Mr笔记

Appearance

S15-02 算法-队列 ​

[TOC]

API ​

队列：

  • enqueue()：(el)，O(1)，入队，向队尾添加元素。
    • el：any，队列中的元素。
  • dequeue()：()，O(1)，出队，移除队首元素，同时返回被移除的元素。
  • front()/peek()：()，O(1)，返回队首元素。
  • isEmpty()：()，判断队列是否为空。
  • size()：()，返回队列中元素的个数。

双端队列：

  • addFront()：(value)，在双端队列的头部添加元素。
  • removeBack()：()，在双端队列的尾部移除元素。

优先级队列：

  • enqueue()：(value, priority)，O(1)，入队，向队尾添加元素。
  • dequeue()：()，O(1)，出队，移除队首元素，同时返回被移除的元素。

队列 Queue ​

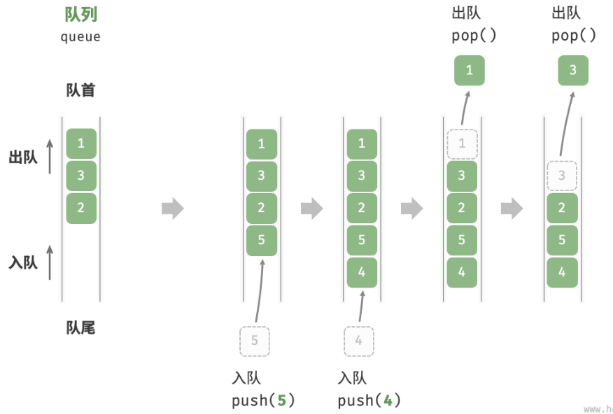
队列(queue)：是一种遵循先入先出规则的线性数据结构。顾名思义，队列模拟了排队现象，即新来的人不断加入队列尾部，而位于队列头部的人逐个离开。

队列头部称为“队首”，尾部称为“队尾”，将把元素加入队尾的操作称为“入队”，删除队首元素的操作称为“出队”。

image-20240614085113221

生活中的队列： 生活中类似队列的场景就是非常多了，比如在电影院买票，商场结账，甚至是厕所排队。优先排队的人，优先处理。

开发中队列的应用：

  • 打印队列：

    • 有五份文档需要打印，这些文档会按照次序放入到打印队列中。

    • 打印机会依次从队列中取出文档，优先放入的文档，优先被取出，并且对该文档进行打印。

    • 以此类推，直到队列中不再有新的文档。

  • 线程队列：

    • 在开发中，为了让任务可以并行处理，通常会开启多个线程。

    • 但是，我们不能让大量的线程同时运行处理任务。 (占用过多的资源)

    • 这个时候，如果有需要开启线程处理任务的情况，我们就会使用线程队列。

    • 线程队列会依照次序来启动线程，并且处理对应的任务。

  • 二叉树的层序遍历： 当然队列还有很多其他应用，我们后续的很多算法中也会用到队列。

队列的实现 ​

队列的实现和栈一样，有两种方案：

  • 基于数组实现

  • 基于链表实现

我们需要创建自己的类，来表示一个队列

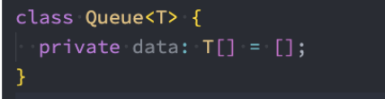
image-20240614115740316

代码解析：

  • 我们创建了一个 Queue 的类，用户创建队列的类，并且是一个泛型类。

  • 在类中，定义了一个变量，这个变量可以用于保存当前队列对象中所有的元素。 (和创建栈非常相似)

  • 这个变量是一个数组类型。

    • 我们之后在队列中添加元素或者删除元素，都是在这个数组中完成的。

  • 队列和栈一样，有一些相关的操作方法，通常无论是什么语言，操作都是比较类似的。

数组实现 ​

1、定义抽象接口

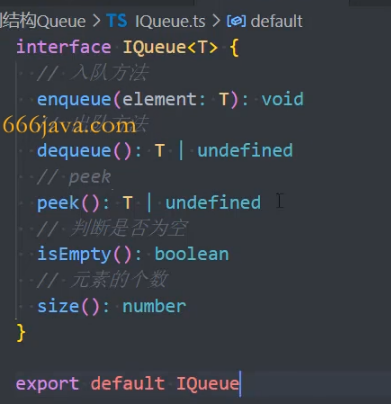
image-20240614112227319

2、实现接口 IQueue

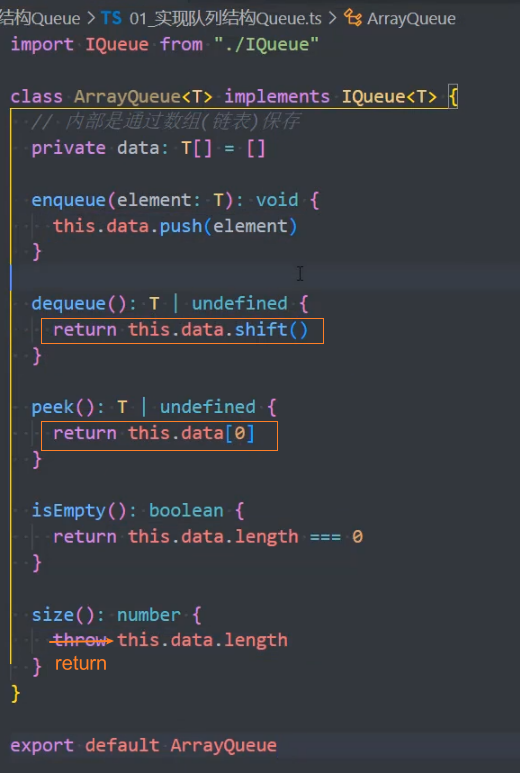
image-20240614112616640

3、测试队列

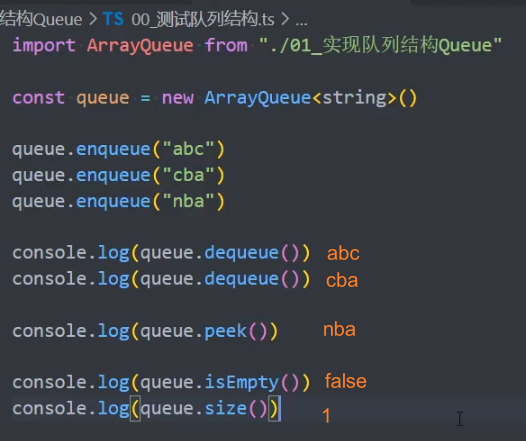
image-20240614112858708

优化： 使用 get 语法，可以将方法当做属性调用

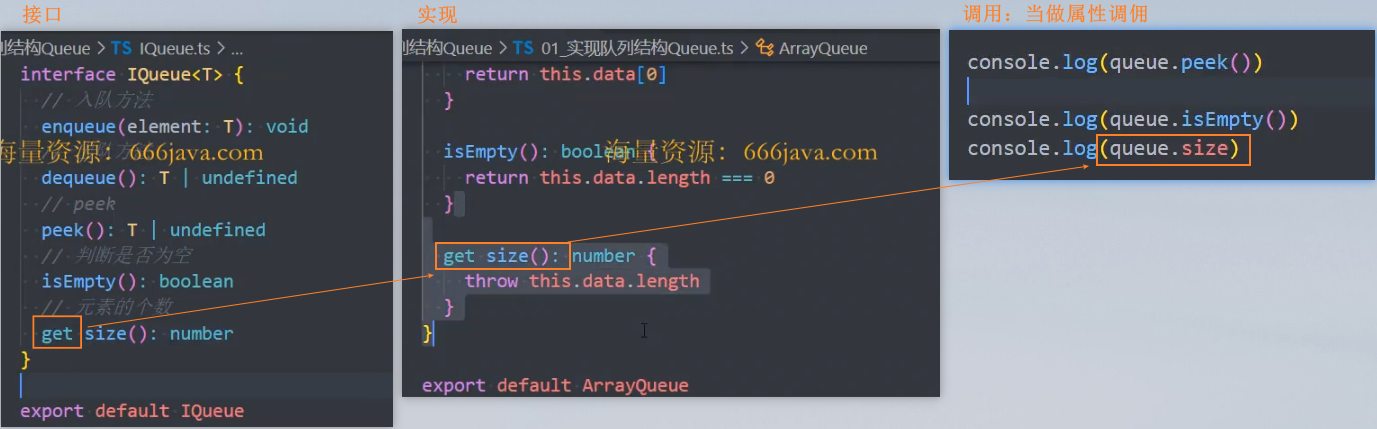
image-20240614113311669

优化： 抽取接口

  • 抽取相同的方法：peek, isEmpty, size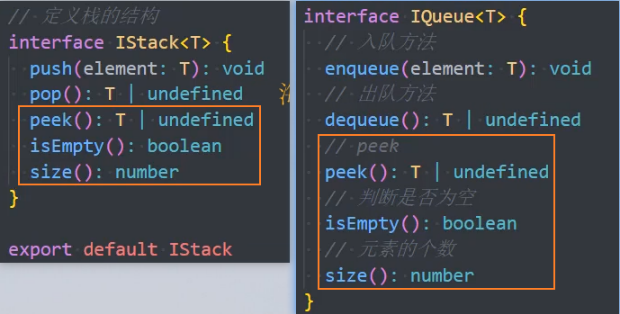

    image-20240614113659092

  • IQueue和IStack继承IList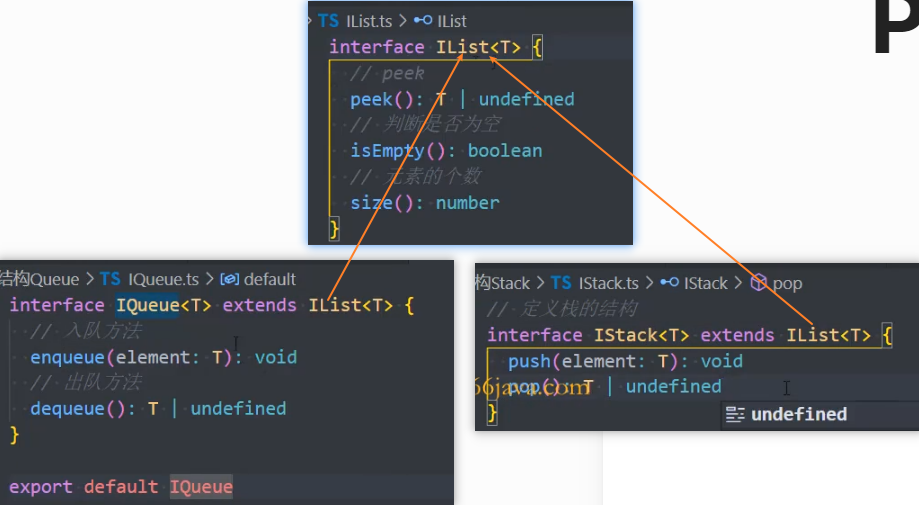

    image-20240614114250856

链表实现【 ​

面试题 ​

击鼓传花 ​

击鼓传花是一个常见的面试算法题： 使用队列可以非常方便的实现最终的结果。

原游戏规则：

  • 班级中玩一个游戏，所有学生围成一圈，从某位同学手里开始向旁边的同学传一束花。

  • 这个时候某个人(比如班长)，在击鼓，鼓声停下的一颗，花落在谁手里，谁就出来表演节目。

修改游戏规则：

  • 我们来修改一下这个游戏规则。

  • 几个朋友一起玩一个游戏，围成一圈，开始数数，数到某个数字的人自动淘汰。

  • 最后剩下的这个人会获得胜利，请问最后剩下的是原来在哪一个位置上的人?

封装一个基于队列的函数：

  • 参数：所有参与人的姓名，基于的数字；

  • 结果：最终剩下的一人的姓名；


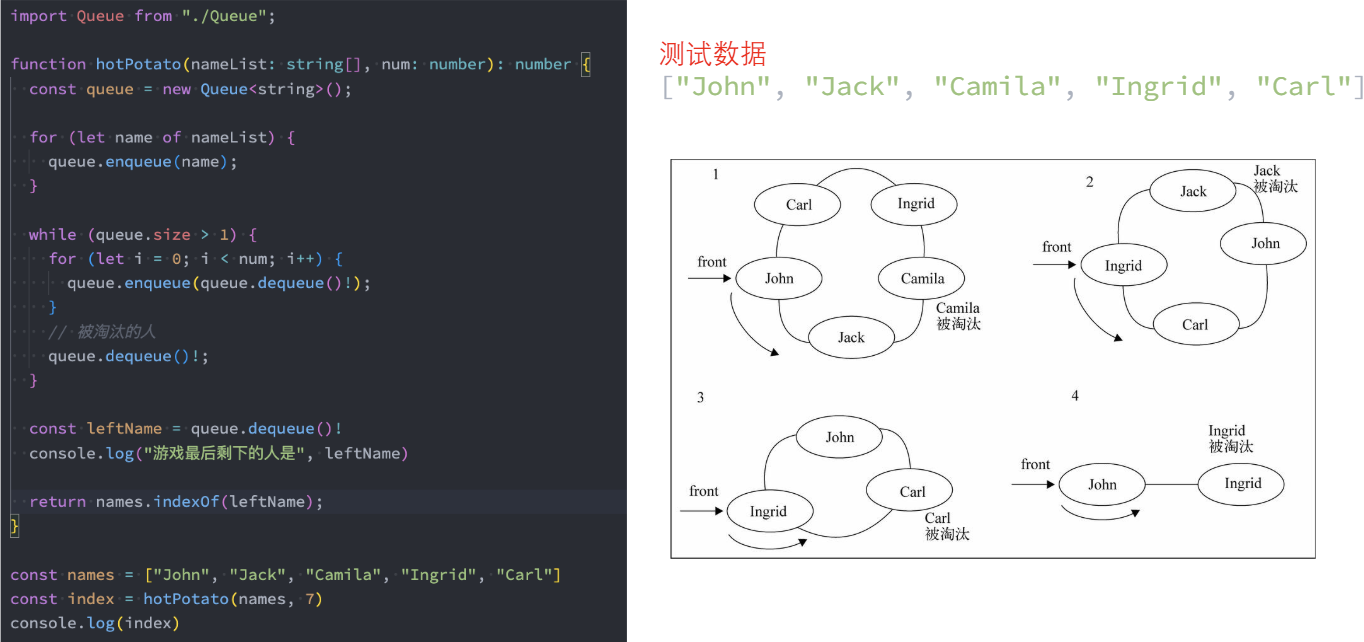
击鼓传花的实现

image-20240614115841637

约瑟夫环 ​

什么是约瑟夫环问题（历史）？

阿桥问题（有时也称为约瑟夫斯置换），是一个出现在计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。

  • 人们站在一个等待被处决的圈子里。

  • 计数从圆圈中的指定点开始，并沿指定方向围绕圆圈进行。

  • 在跳过指定数量的人之后，处刑下一个人。

  • 对剩下的人重复该过程，从下一个人开始，朝同一方向跳过相同数量的人，直到只剩下一个人，并被释放。

  • 在给定数量的情况下，站在第几个位置可以避免被处决？

这个问题是弗拉维·奥约瑟夫命名的，他是 1 世纪的一名犹太历史学家。

  • 他在自己的日记中写道，他和他的 40 个战友被罗马军队包围在洞中。

  • 他们讨论是自杀还是被俘，最终决定自杀，并以抽签的方式决定谁杀掉谁。


约瑟夫环问题 – 字节、阿里、谷歌等面试题

击鼓传花和约瑟夫环其实是同一类问题，这种问题还会有其他解法（后续讲解）

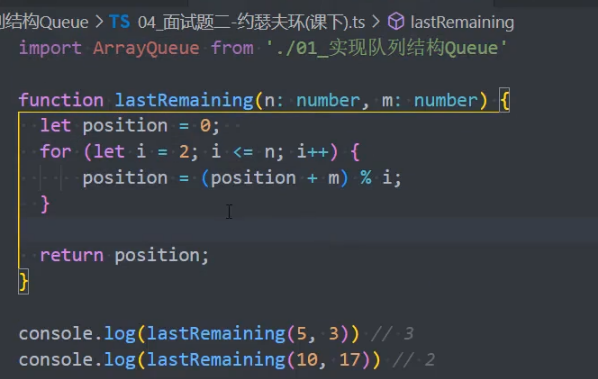
  • 0,1,···,n-1 这 n 个数字排成一个圆圈，从数字 0 开始，每次从这个圆圈里删除第 m 个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

  • 例如，0、1、2、3、4 这 5 个数字组成一个圆圈，从数字 0 开始每次删除第 3 个数字，则删除的前 4 个数字依次是 2、0、4、1，因此最后剩下的数字是 3。

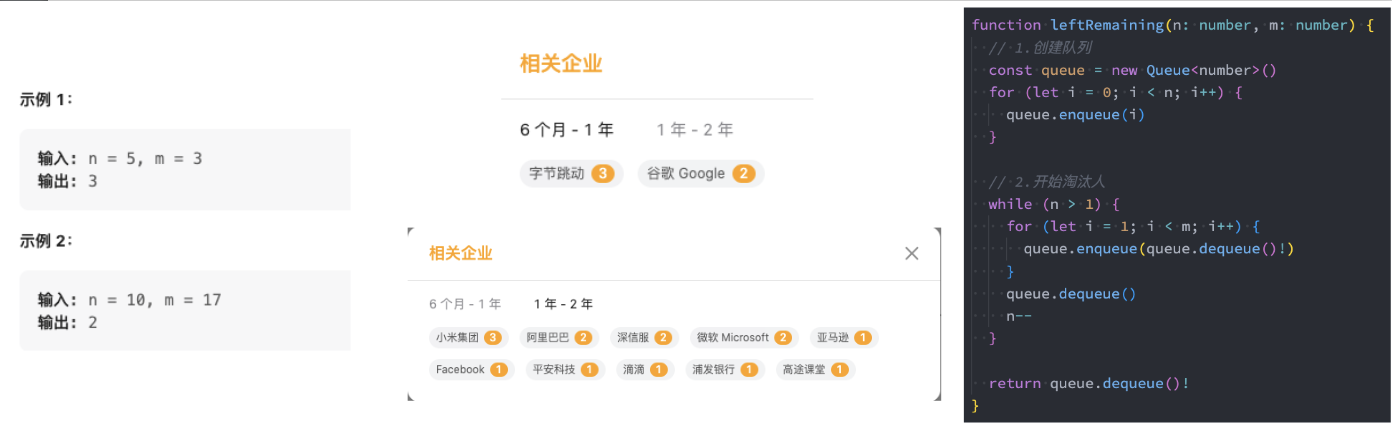
image-20240614120047612

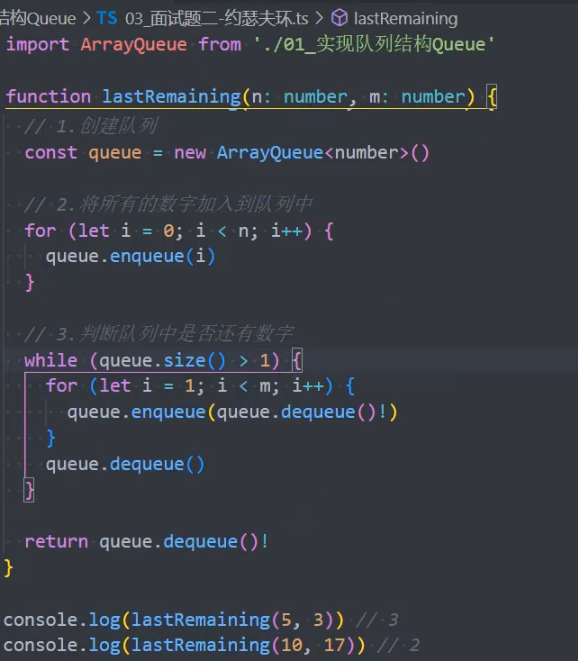
image-20240614151117825

优化： 上述使用数组实现的队列来解决该面试题，性能并不高。使用 动态规划 的方法更优

image-20240614151414317

双端队列 Deque ​

概述 ​

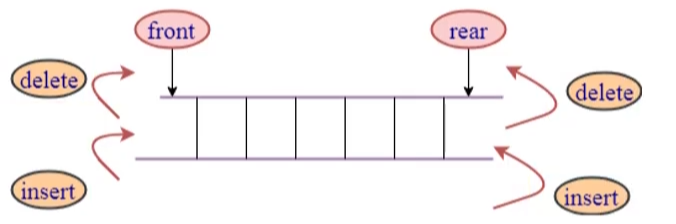
双端队列(Deque，Double-Ended Queue) 是一种允许在队列的两端进行插入和删除操作的数据结构。

前端我们已经学习了队列结构，它是一种受限的线性结构，并且限制非常的严格。

双端队列因为解除了一部分限制，所以在解决一些特定问题时会更加的方便；

image-20250127110735372


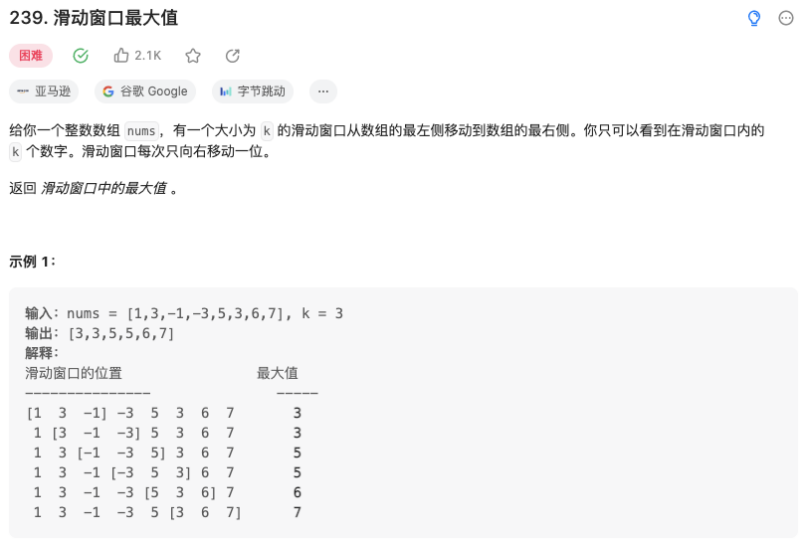
滑动窗口最大值【 ​

image-20250123120055748

双端队列的实现 ​

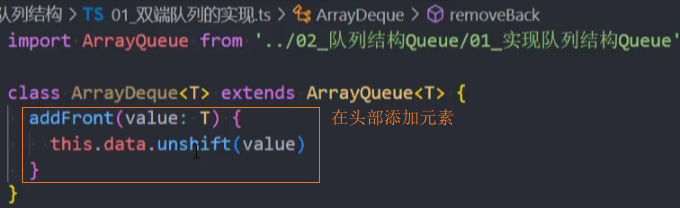
封装-addFront() ​

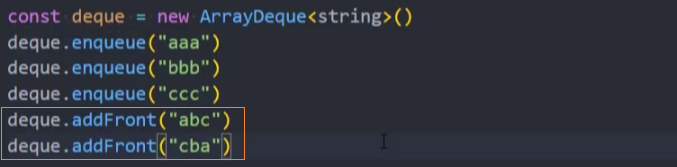
addFront()：(value)，在双端队列的头部添加元素。

image-20250127112116073

测试：

image-20250127112501428

封装-removeBack() ​

removeBack()：()，在双端队列的尾部移除元素。

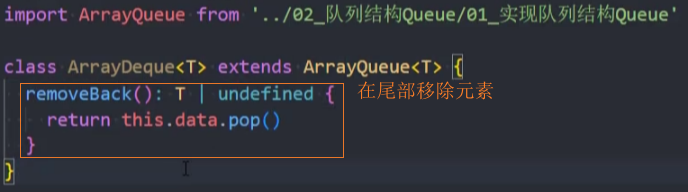
image-20250127112233684

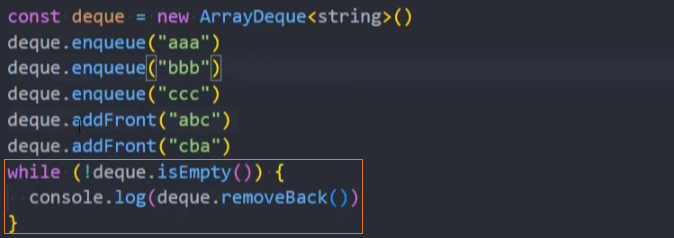
测试：

image-20250127112528655

优先级队列 Priority Queue ​

概述 ​

优先级队列(Priority Queue) 是一种特殊的队列数据结构，它的核心特性是，每个元素都有一个优先级，队列中的元素按照优先级顺序进行处理。

实现方式： 优先级队列可以用数组、链表等数据结构来实现，但最常用的方式是堆，通常选择 最小堆 或 最大堆。


应用场景：

机场登机顺序：

  • 头等舱和商务舱乘客的优先级要高于经济舱乘客。
  • 在有些国家，老年人和孕妇（或带小孩的妇女）登机时也享有高于其他乘客的优先级。

医院的（急诊科）候诊室：

  • 医生会优先处理病情比较严重的患者。
  • 一般情况下是按照排号的顺序。

计算机中的线程：

  • 我们也可以通过优先级队列来重新排序队列中任务的顺序。

  • 比如每个线程处理的任务重要性不同, 我们可以通过优先级的大小, 来决定该线程在队列中被处理的次序。

优先级队列的实现 ​

优先级队列的实现有两种方式：

  • 方式一：创建优先级的节点，保存在堆结构中。
  • 方式二：数据自身返回优先级的比较值。

实现方式一 ​

方式一：创建优先级的节点，保存在堆结构中。

封装-PriorityNode ​

image-20250127114958596

image-20250127114933414

封装-PriorityQueue ​

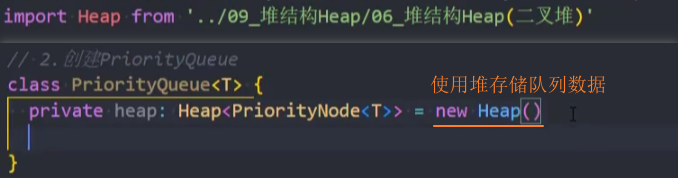
image-20250127115326106

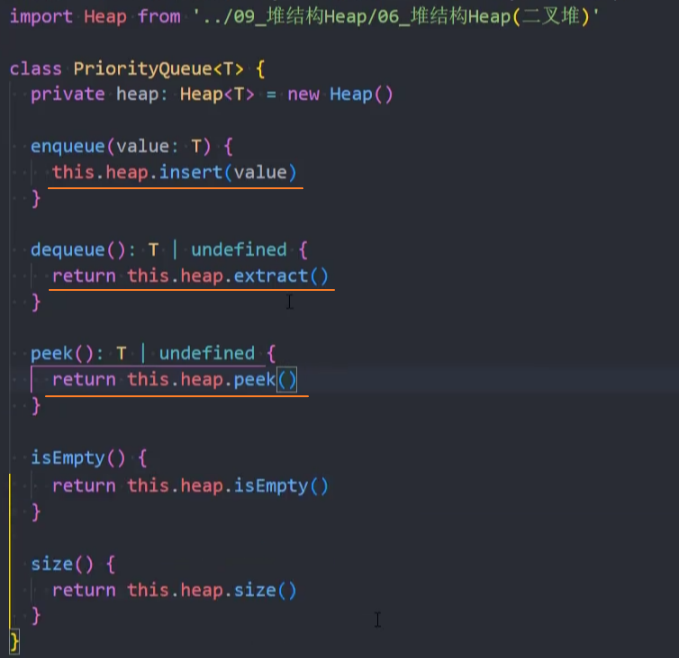
封装-enqueue() ​

enqueue()：(value, priority)，O(1)，入队，向队尾添加元素。

实现思路：根据传入的value和priority创建一个Node实例，并插入该Node实例

image-20250127120329473

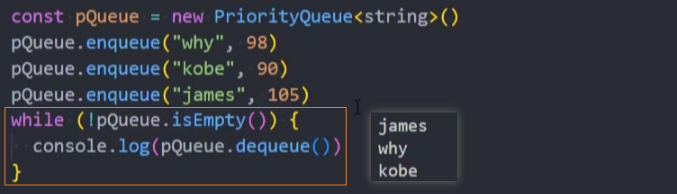
测试：

image-20250127115742764

封装-dequeue() ​

dequeue()：()，O(1)，出队，移除队首元素，同时返回被移除的元素。

image-20250127115923047

测试：

image-20250127120257190

封装-peek() ​

image-20250127120012590

封装-isEmpty() ​

image-20250127120037478

封装-size() ​

image-20250127120053562

实现方式二 ​

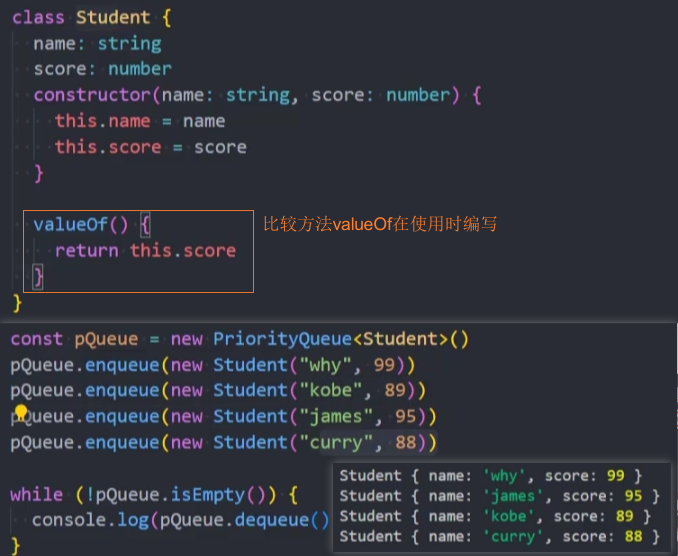
方式二：数据自身返回优先级的比较值。

思路：

  • 1、在PriorityQueue类中直接插入对象。
  • 2、对象的优先级比较则是在使用时通过valueOf()进行。

image-20250127121905054

测试：

image-20250127122150293